Fractal Art and Sierpinski Triangles
Sierpinski Triangle going from 4 (4*1) to 65,536 (4**8) triangles
A Sierpinski Triangle is a fractal that is generated by recursively subdividing an equilateral triangle into four smaller equilateral triangles. Starting with one triangle, we divide it into four equilateral triangles. Three of these triangles will “point up”. One will point down.
We then divide each of those four triangles into four more triangles. With each generation, the number of triangles increases by a factor of four while the triangles' size decreases by a factor of four.
How to code this?
There are two steps to coding this.
- The data and display problems: how to store and draw the triangles that we generate?
- The geometry problem: how to subdivide the triangle and generate smaller triangles? We need an object that constitutes a triangle, and that object should have a method to divide itself into four smaller triangles.
We’ll tackle them in order.
Data Structure & Display
We’ll create an object to hold a triangle and a smaller object to hold a point (x and y coordinate).
var Point = function (x, y) {
this.x = x;
this.y = y;
};
var Triangle = function (args = {}) {
const { A, B, C, tIndex } = args;
this.A = new Point(A[0], A[1]);
this.B = new Point(B[0], B[1]);
this.C = new Point(C[0], C[1]);
this.tIndex = tIndex;
let xDiff = this.B.x - this.A.x;
let yDiff = this.B.y - this.A.y;
this.sLength = Math.sqrt(Math.pow(xDiff, 2) + Math.pow(yDiff, 2));
};
A, B, and C are the three points corresponding to the sides of the triangle. For simplicity, we’ll define these points in terms of the left-most, bottom-most point of the triangle, proceeding clockwise around the triangle from there. So, for a triangle that points up, A is the bottom-left, B is the top point, and C is the bottom-right. For a triangle that points down, A is the bottom, B the top-left, and C the top-right.
tIndex might not make sense right now. We’re indexing each triangle from 1 to 4 to keep track of which triangle is drawn differently (the “blank space”) when we draw the fractal.
We calculate sLength with the distance formula. It doesn’t matter which two points we pick to measure the distance between, because all the sides are the same length.
We draw the triangles in the same manner that we define the points. Index 1 is the bottom-left triangle. 2 is the top. 3 is the down-pointing inner triangle, and 4 is the bottom-right triangle.
We’re using HTML5 Canvas to draw the triangles. It’s pretty basic. You put a canvas element in your HTML like this:
<canvas id="gasket_0" width="500" height="500"></canvas>
Then, in your JS, you select the canvas and call getContext('2d').
const C = document.getElementById("gasket_0");
const ctx = C.getContext("2d");
The context is what you use to draw to the canvas.
To draw lines, we tell the context that we are beginning a “path” with ctx.beginPath();. Then, we can call moveTo with an X and Y coordinate to move our virtual “pen” to this point. We can call lineTo with another X and Y coordinate to draw a line connecting these two points.
So, to draw a triangle that points up, we’ll moveTo the first point A, draw a line to the point B, draw a line from B to C, and then draw a line from C back to A, where we started.
We can set the fillStyle of the context, depending on which triangle we are drawing. This is where the tIndex comes in. We can define the BLANK_SPACE_COLOR to be whatever we like (hex values, CSS color names, and rgb strings are all accepted).
I’m using tinyColor to grab some neat colors by “spinning” the hue by a random amount and turning that color into an rgb string for the context.
When we’ve defined the path and fill color, we call ctx.fill() to complete the drawing.
Triangle.prototype.draw = function (ctx) {
ctx.beginPath();
ctx.moveTo(this.A.x, this.canvasY(this.A.y));
ctx.lineTo(this.B.x, this.canvasY(this.B.y));
ctx.lineTo(this.C.x, this.canvasY(this.C.y));
ctx.lineTo(this.A.x, this.canvasY(this.A.y));
if (this.tIndex == 3) {
ctx.fillStyle = BLANK_SPACE_COLOR;
} else {
let baseColor = tinycolor(random_rgba());
ctx.fillStyle = baseColor
.spin(Math.random() * 10)
.lighten(5)
.toRgbString();
}
ctx.fill();
};
Here’s the tricky thing about canvas. The origin is the top-left corner of the canvas. This means that your X values work as you’d expect: 0 is far left, and canvas.width is far right. Y values, however, increase when going down. It’s as though you’re in the fourth quadrant of a standard graph.
When I initialize the gasket, I add a canvasY method to the prototype chain of Triangle. All this does is subtracts the the y coordinate I’m drawing from the gasketHeight so that I can define y=0 at the bottom instead of the top. This was just a personal choice to make things easier to reason about.
Geometry
If it’s been a while since you’ve had a geometry class, you might have forgotten a few key properties of an equilateral triangle. All the sides are equal. The height of the triangle is given by sideLength*sqrt(3)/2.
This is where it all comes together. We need to write a function that will split any triangle in the gasket into four equal equilateral triangles.
The easiest way to go about this is to draw a triangle on paper and think through things.
Here’s the picture I drew:
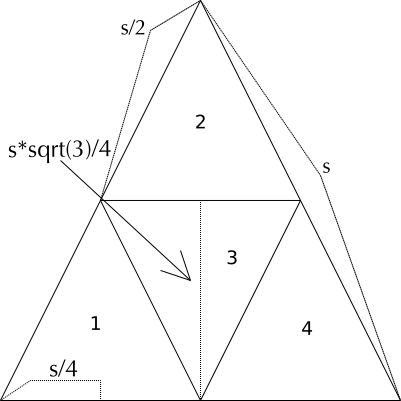
Let’s walk through coding this function triangle by triangle based on the picture.
The key point to note is that when we generate these smaller triangles, we define the triangles' coordinates in terms of the bottom-left point of the original triangle. This means that we have to offset the other points in the triangle by this.A.x and this.A.y.
If we did not do this, things would work fine for the first four triangles (because this.A.x and this.A.y are zero, and adding zero changes nothing) and then go haywire on subsequent triangles.
Triangle.prototype.fourSmaller()
Triangle One
const sLength = this.getLength();
const lRoot3 = Math.sqrt(3) * sLength;
let tOne = new Triangle({
// bottom-left
A: [this.A.x, this.A.y],
B: [this.A.x + sLength / 4, this.A.y + lRoot3 / 4],
C: [this.A.x + sLength / 2, this.A.y],
tIndex: 1,
});
We set up some constants and then define the coordinates of the bottom-left triangle, #1 from the picture.
- A: Bottom-left point is going to be just the A.x and A.y of the starting triangle.
- B: The top point is going to be halfway up the original triangle, and a quarter of the way across.
- C: The bottom-right point will be halfway across the original triangle, and at the starting height.
Triangle Two
let tTwo = new Triangle({
// top
A: [this.A.x + sLength / 4, this.A.y + lRoot3 / 4],
B: [this.A.x + sLength / 2, this.A.y + lRoot3 / 2],
C: [this.A.x + sLength * (3 / 4), this.A.y + lRoot3 / 4],
tIndex: 2,
});
- A: Bottom-left point is going to be the same as point B of Triangle One
- B: The top point is going to be halfway up the original triangle, and a half of the way across.
- C: The bottom-right point will be three-quarters of the way across the original triangle, and at the starting height.
Triangle Three (the upside-down one)
let tThree = new Triangle({
// middle (down-pointing)
A: [this.A.x + sLength / 2, this.A.y],
B: [this.A.x + sLength / 4, this.A.y + lRoot3 / 4],
C: [this.A.x + sLength * (3 / 4), this.A.y + lRoot3 / 4],
tIndex: 3,
});
- A: Bottom point is going to be the midpoint of the starting triangle
- B: The top-left point is going to be one-quarter across the original triangle, and halfway up
- C: The top-right point will be three-quarters across the original triangle, and at the starting height.
Triangle Four
let tFour = new Triangle({
// top
A: [this.A.x + sLength / 2, this.A.y],
B: [this.A.x + sLength * (3 / 4), this.A.y + lRoot3 / 4],
C: [this.A.x + sLength, this.A.y],
tIndex: 4,
});
- A: Bottom-left point is going to be the same as the bottom point of Triangle Three
- B: The top point is going to be three-quarters across the original triangle, and halfway up
- C: The bottom-right point will be all the way across the original triangle, and at the starting height.
Note a lot of shared points here. Point A of #2 is Point B of #1. Point A of #3 is Point C of #1, etc.
Initialization and Triangle Generation
We set up some basic constants and create the urTriangle, the triangle that will spawn all the smaller triangles.
const gasketWidth = 500; // px
const padding = 10; // px
const gasketHeight = (Math.sqrt(3) * gasketWidth) / 2;
const canvas = document.getElementById("gasket_" + id);
canvas.width = gasketWidth + padding * 2;
canvas.height = gasketHeight + padding * 2;
const urTriangle = new Triangle({
A: [0, 0],
B: [gasketWidth / 2, gasketHeight],
C: [gasketWidth, 0],
});
let ctx = canvas.getContext("2d");
ctx.translate(padding, padding);
ctx.imageSmoothingEnabled = true;
The ctx.translate moves the drawing context to account for our padding, and ctx.imageSmoothingEnabled helps with anti-aliasing and makes things look a bit smoother.
Then I do this:
Triangle.prototype.canvasY = (Y) => gasketHeight - Y;
urTriangle.draw(ctx);
pics.push(ctx.getImageData(0, 0, canvas.width, canvas.height));
let triangles = urTriangle.fourSmaller();
triangles.forEach((t) => t.draw(ctx));
pics.push(ctx.getImageData(0, 0, canvas.width, canvas.height));
We’ve got the first four! Now just get the next 65,532…
Wait, getImageData? pics?
I wanted to watch the fractals' triangle number expand and contract in an infinite loop. I did not want to have to recalculate the frames, however.
I use getImageData to save off the data on the canvas at each level of drawing in pics. I then set an interval to display these saved off datasets using putImageData. I set the interval to “bounce” back and forth (changing direction to backwards when it reaches either end of the array).
Finally, I call ctx.clearRect, in between each putImageData a very useful function. You pass it the starting X and Y coordinates, followed by the width and height of the rectangle.
const levels = 7;
for (var i = 1; i <= levels; i++) {
triangles = triangles
.map((t) => t.fourSmaller())
.reduce((arr, c) => arr.concat(c), []);
triangles.forEach((t) => t.draw(ctx));
pics.push(ctx.getImageData(0, 0, canvas.width, canvas.height));
}
var ct = 0;
var direction = id % 2 == 0 ? 1 : -1;
setInterval(() => {
if (ct == pics.length - 1) {
direction = -1;
}
if (ct === 0) {
direction = 1;
}
ct += direction;
ctx.clearRect(0, 0, canvas.width, canvas.height);
ctx.putImageData(pics[ct], 0, 0);
}, 250);
warning
levels should not exceed 7, or 4**(levels+1) => 65,536 triangles. If you do…well, let’s just say that if you’re in CodePen, you can add ?turn_off_js=true (Docs) to the end of your URL so that you can access the pen and fix the code. It will hang hard. I suspect this is caused by compounded roundoff error and HTML5 canvas weirdness when you try to draw >100k elements with poor precision.
TIL
Fractal patterns can be generated by the iterated division of space according to a rule, known formally as an Iterated function system. Try creating the Sierpinski Carpet or other Rep-tiles like the Koch Snowflake. Have fun with it. Soon we will cover Binary Space Partitioning, a method of dividing space that can be used for the procedural generation of game levels, like in my Roguelike Dungeoncrawler.